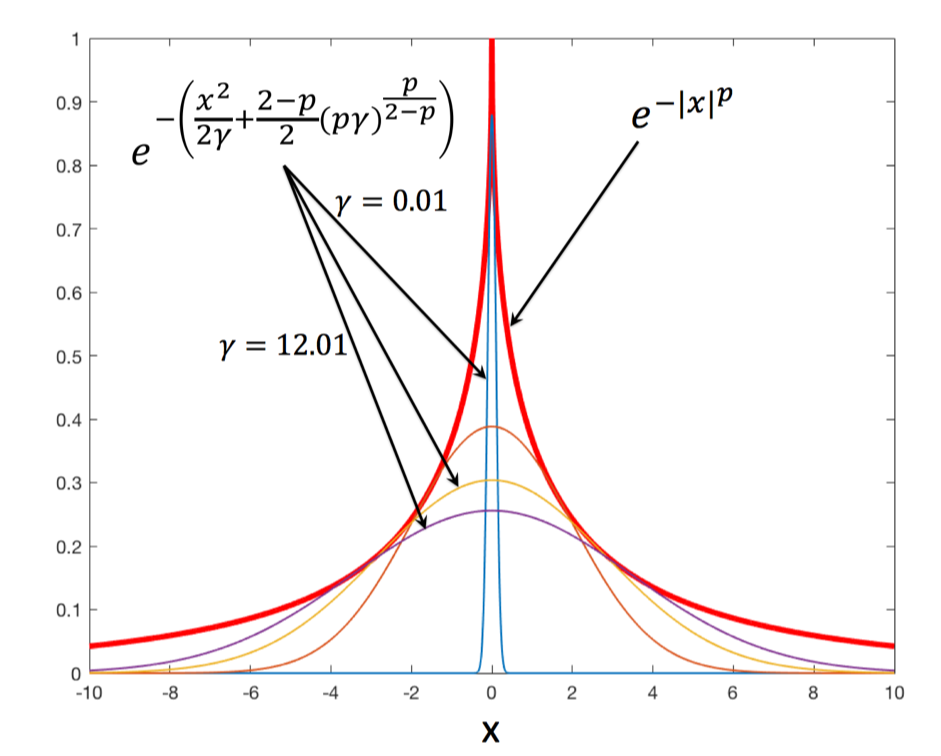

Several sparse regularization techniques have been proposed and evaluated for detecting epicardial and transmural infarcts. But their performance on non-transmural, especially endocardial infarcts, is not fully explored. Here, we first show that the detection of non-transmural endocardial infarcts presents severe difficulty to the prevalent sparse algorithms like L1 norm or total variation regularization. Subsequently, we propose a sparse regularization technique based on a variational approximation of L0 norm- by using Legendre-Fenchel duality of convex functions. We demonstrate that the presented method outperforms existing algorithms by a descent margin, particularly when infarction is entirely on the endocardium.